Variance

In probability and statistics, the variance of a random variable is the average value of the square distance from the mean value. It represents the how the random variable is distributed near the mean value. Small variance indicates that the random variable is distributed near the mean value. Big variance indicates that the random variable is distributed far from the mean value. For example, with normal distribution, narrow bell curve will have small variance and wide bell curve will have big variance.

Variance definition

The variance of random variable X is the expected value of squares of difference of X and the expected value μ.

σ² = Var ( X ) = E [( X- μ)²]

From the definition of the variance we can get

σ² = Var ( X ) = E(X²) - μ²

Variance of continuous random variable

For continuous random variable with mean value μ and probability density function f(x):

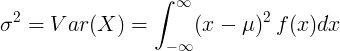
$\sigma ^2=Var(X)=\int_{-\infty }^{\infty }(x-\mu)^2\: f(x)dx$

or

$Var(X)=\left [ \int_{-\infty }^{\infty }x^2\: f(x)dx \right ]-\mu^2$

Variance of discrete random variable

For discrete random variable X with mean value μ and probability mass function P(x):

$\sigma ^2=Var(X)=\sum_{i}^{}(x_i-\mu _X)^2P_X(x_i)$

or

$Var(X)=\left [ \sum_{i}^{}x_i^2P(x_i) \right ]-\mu^2$

Properties of variance

When X and Y are independent random variables:

Var(X+Y) = Var(X) + Var(Y)

Standard deviation►