Convolution
Convolution is the correlation function of f(τ) with the reversed function g(t-τ).
The convolution operator is the asterisk symbol * .
- Continuous convolution
- Discrete convolution
- 2D discrete convolution
- Filter implementation with convolution
- Convolution theorem
Continuous convolution
The convolution of f(t) and g(t) is equal to the integral of f(τ) times f(t-τ):
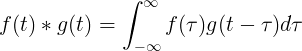
Discrete convolution
Convolution of 2 discrete functions is defined as:
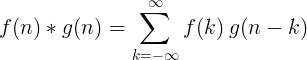
2D discrete convolution
2 dimensional discrete convolution is usually used for image processing.
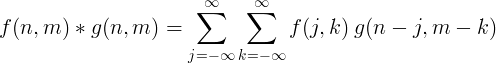
Filter implementation with convolution
We can filter the discrete input signal x(n) by convolution with the impulse response h(n) to get the output signal y(n).
y(n) = x(n) * h(n)
Convolution theorem
The Fourier transform of a multiplication of 2 functions is equal to the convolution of the Fourier transforms of each function:
ℱ{f ⋅ g} = ℱ{f} * ℱ{g}
The Fourier transform of a convolution of 2 functions is equal to the multiplication of the Fourier transforms of each function:
ℱ{f * g} = ℱ{f} ⋅ ℱ{g}
Convolution theorem for continuous Fourier transform
ℱ{f (t) ⋅ g(t)} = ℱ{f(t)} * ℱ{g(t)} = F(ω) * G(ω)
ℱ{f (t) * g(t)} = ℱ{f(t)} ⋅ ℱ{g(t)} = F(ω) ⋅ G(ω)
Convolution theorem for discrete Fourier transform
ℱ{f (n) ⋅ g(n)} = ℱ{f(n)} * ℱ{g(n)} = F(k) * G(k)
ℱ{f (n) * g(n)} = ℱ{f(n)} ⋅ ℱ{g(n)} = F(k) ⋅ G(k)
Convolution theorem for Laplace transform
ℒ{f (t) * g(t)} = ℒ{f(t)} ⋅ ℒ{g(t)} = F(s) ⋅ G(s)